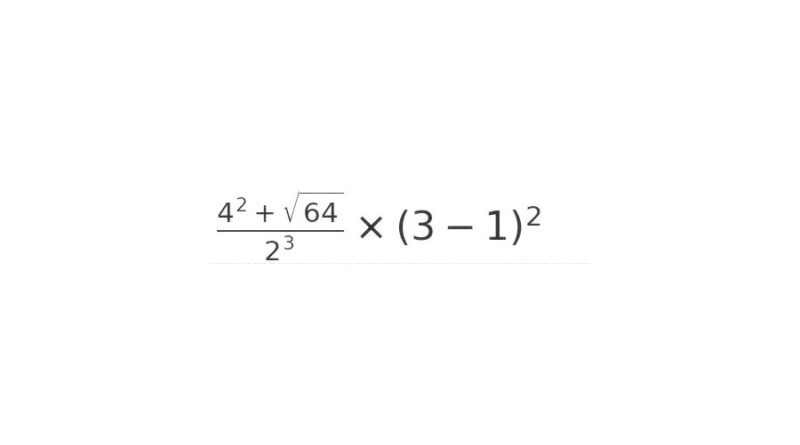Zagadka Matematyczna – oblicz – czy dasz radę?
Każda część tego wyrażenia matematycznego ma swoje unikalne miejsce i znaczenie, a razem tworzą one wyrażenie, które jest nie tylko wyzwaniem obliczeniowym, ale także przykładem matematycznej estetyki. Od kwadratu liczby 4, przez pierwiastek kwadratowy z 64, po dzielenie przez 8 i mnożenie przez kwadrat różnicy liczb 3 i 1, każdy krok w tym działaniu przypomina o fundamentalnych operacjach, które są podstawą matematyki.
To działanie jest niczym matematyczna symfonia, gdzie każdy element ma swoją rolę, a ich współdziałanie prowadzi do końcowego wyniku, który jest bardziej niż sumą jego części. Jest to przypomnienie, że matematyka, w swojej istocie, jest językiem opisującym wzory i związki w świecie wokół nas, a także wewnętrzną strukturę logicznego myślenia.
Poznaj także:
Zagadka matematyczna, 6÷2(2+1)= oblicz – zasady kolejności wykonywania działań
W ten sposób, prezentowana wizualizacja nie tylko pokazuje konkretne działanie matematyczne, ale także inspiruje do docenienia piękna i głębi matematyki, zachęcając do dalszego odkrywania jej tajemnic i zastosowań.
\[ \frac{4^2 + \sqrt{64}}{2^3} \times (3 – 1)^2 \]
Rozwiązanie krok po kroku
- Potęgowanie: Najpierw obliczamy \(4^2\). Ponieważ \(4 \times 4 = 16\), wynik to \(16\). Następnie obliczamy \(2^3\), co daje \(2 \times 2 \times 2 = 8\).
- Pierwiastkowanie: Następnie obliczamy pierwiastek kwadratowy z \(64\), który wynosi \(8\), ponieważ \(8 \times 8 = 64\).
- Dodawanie w liczniku: Teraz dodajemy wyniki potęgowania i pierwiastkowania: \(16 + 8\), co daje nam \(24\).
- Obliczenie wartości ułamka: Dzielimy sumę uzyskaną w liczniku przez \(2^3\), czyli \(8\), co daje nam \(3\), ponieważ \(24 \div 8 = 3\).
- Działania w nawiasie i potęgowanie: Obliczamy wartość wyrażenia w nawiasie, \(3 – 1\), co daje \(2\), a następnie podnosimy wynik do kwadratu, czyli \(2^2 = 4\).
- Mnożenie wyników: W końcu, mnożymy wynik z ułamka \(3\) przez wynik potęgowania \(4\), co daje nam ostateczny wynik \(12\).
Wynik
Całkowity wynik wyrażenia to 12.